Regression How Do You Decide Which Transformation Is Best

By Jo_Crystal663 17 May, 2022 Post a Comment

Like Ariel Linden indicated there are many software packages that will perform these tests for you. Without any information other than that r appears always to be positive a good choice is to explore the Box-Cox transformations r r p 1 p for various powers p usually chosen to be multiples of 1 2 or 1 3 and typically between 1 and 1.

4 6 3 3 Transformations To Improve Fit

Transforming before multilevel modeling thus attempting to make coefficients more comparable thus allowing more effective second-level regressions which in turn improve partial pooling.

. In order to account for this interaction the equation of linear regression should be changed from. With backward elimination you can deselect features that have p_values 005 which is interpreted as a failure to explain the change in the target other than chance. The main positive is that nonlinear regression provides the most flexible curve-fitting functionality.

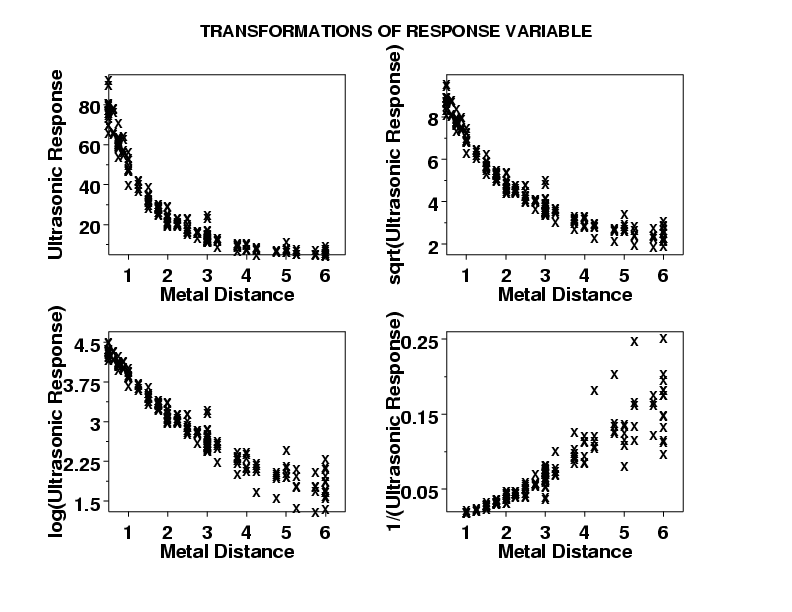
Generally you choose the models that have higher adjusted and predicted R-squared values. Mosteller and Tukey suggested looking at the plot of untransformed X and Y matching the curve that you see to one of the four quadrant curves in the diagram and applying an indicated transformations taking. Plots of raw data and residuals can also be informative when considering transformations as with the log transformation for arsenic levels in Section 56.

2 BestEquation Name -25 to -15 1y2inverse square -15 to -075 1yreciprocal -075 to -025 1 p yinverse square root -025 to 025 lny natural log 025 to 075 p ysquare root 075 to 15ynone 15 to 25y2square Example. Help meet assumptions In your case of a linear regression you have several assumptions that you have to meet including things like linearity and residuals have a constant variance and appear independent of each other. Instead we are comparing only how constant the variation within each plot is for these four plots.

Y e c 2 e c 1 x. To introduce basic ideas behind data transformations we first consider a simple linear regression model in which. If you have a continuous dependent variable linear regression is probably the first type you should consider.

Given several models with similar explanatory ability the simplest is most likely to be the best choice. Mosteller and Tukey 1977 offered their bulging rule suggesting transformations of X or Y based on eyeballing the shape of the untransformed relationship. Start simple and only make the model more complex as needed.

Y x y x. Unlike linear regression you also need to supply starting values for the nonlinear algorithm. Having found the coefficient vector c the best fitting curve is.

When building a Linear Regression model theres no need to include unnecessary features that do not contribute reasonably to the change in the target variable. Therefore slope is 180100 or 18. Rise over the same part of the line is 212-32 or 180.

Run is degrees C or zero to 100 or 100. When creating linear regression models and working with scatterplots we give R the formula. We transform the predictor x values only.

We transform the predictor x values only. We transform the response y values only. Adjusted R-squared and Predicted R-squared.

We can write the equation for the linear transformation Y3218X or F3218C. Transforming your response can help make your relationship more linear and help with your residual assumptions while a transformation on. Deciding which variable goes on the y-axis and which variable goes on the x-axis is tricky.

It illustrates how much variation is explained by your model. See the Topic 61 Linear Regression. Now find the least-squares curve of the form c 1 x c 2 which best fits the data points x i φ i.

The regression problems that we deal with will use a line to transform values of X to predict values of Y. Linear models are the most common and most straightforward to use. Given those results choose the best transformation according to the following table.

If you only use one input variable the adjusted R2 value gives you a good indication of how well your model performs. The more complex you make your model the more likely it is that you are tailoring the model to your dataset specifically and generalizability suffers. You should decide which interaction terms you want to include in the model BEFORE running the model.

We transform the response y values only. The plot with the most constant variation will indicate which transformation is best. To introduce basic ideas behind data transformations we first consider a simple linear regression model in which.

Based on constancy of the variation in the residuals the square root transformation is probably the best tranformation to use for this data. Trying different interactions and keeping the ones. Y β 0 β 1 X 1 β 2 X 2 β3X1X2 ε.

Take the logarithm of the y values and define the vector φ φ i logy i. It penalizes too many input factors and favors parsimonious models. Linear model that uses a polynomial to model curvature.

Y β 0 β 1 X 1 β 2 X 2 ε. These statistics are designed to avoid a key problem with regular R-squared it increases every time you add a predictor and can trick you into specifying an overly complex model. There are some special options available for linear regression.

For example the TRANSREG procedure in SAS will determine the most appropriate transformation. The downside is that it can take considerable effort to choose the nonlinear function that creates the best fit for the particular shape of the curve. We will use algebra and linear regression.

Regression models which are chosen by applying automatic model-selection techniques eg stepwise or all-possible regressions to large numbers of uncritically chosen candidate variables are prone to overfit the data even if the number of regressors in the final model is small. We transform both the predictor x values and response y values. The convention is to use the variable that we think is doing the explaining on the horizontal x.

In contrast to the simple R2 the adjusted R2 takes the number of input factors into account. We transform both the predictor x values and response y values.

Data Transformation

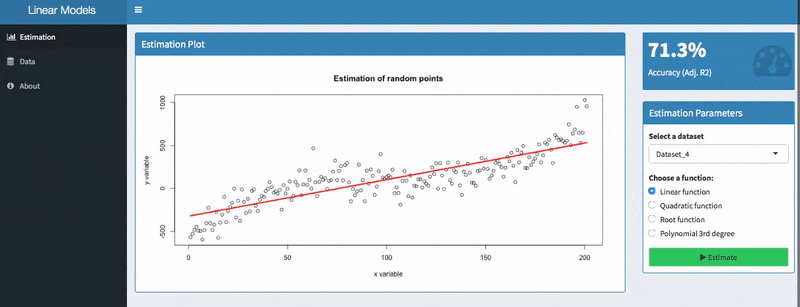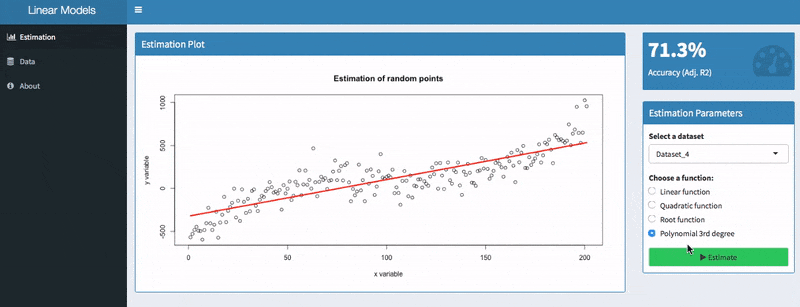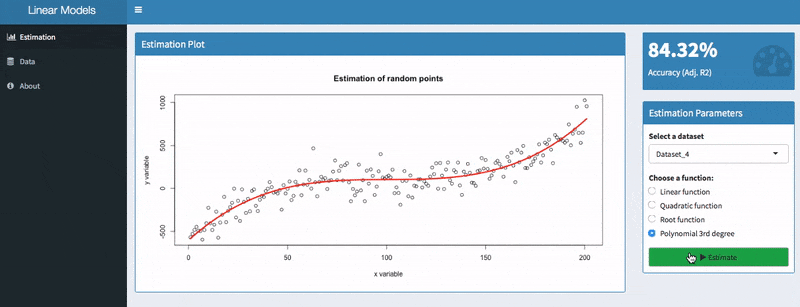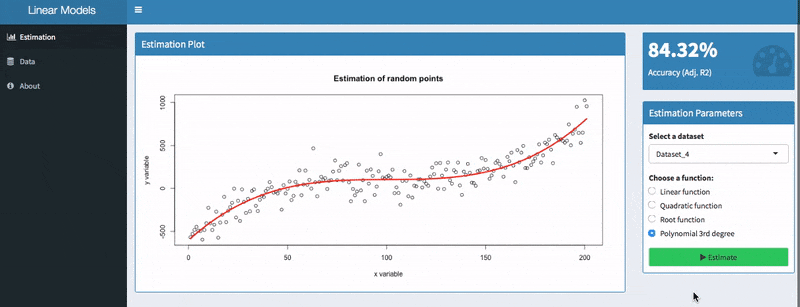
Learn How To Select The Best Performing Linear Regression For Univariate Models